Fatigue Behavior and Life Prediction of Structural Metallic Materials
Fatigue failure is a predominant mode of in-service failure for structural metallic components subjected to cyclic loading. Understanding the fatigue behavior and accurately predicting the fatigue life of metals are critical for ensuring the safety, reliability, and longevity of engineering structures such as aircraft, bridges, and power generation equipment. This article delves into the fundamental mechanisms of metal fatigue, the factors influencing it, and the methodologies employed for life prediction.
1. Fundamentals of Metal Fatigue
Fatigue is a process of progressive, localized, and permanent structural change occurring in a material subjected to conditions that produce fluctuating stresses and strains at some point or points. These changes may culminate in cracks or complete fracture after a sufficient number of fluctuations. The process is generally divided into three stages:
1.1 Crack Initiation
This initial stage involves the nucleation of a microscopic crack, typically at a stress concentration site like a notch, inclusion, or grain boundary. Under cyclic loading, localized plastic deformation occurs, leading to the formation of persistent slip bands (PSBs) on the material's surface, which act as precursors to cracks.
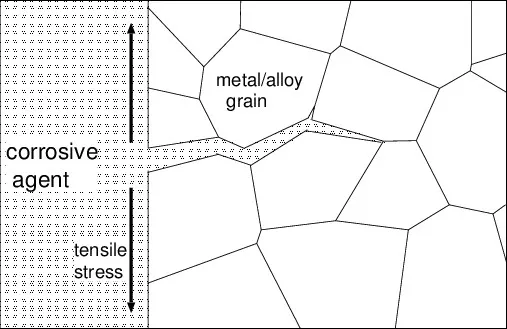div class="caption">Figure 1: Schematic of fatigue crack initiation at a grain boundary caused by irreversible cyclic slip.
1.2 Crack Propagation
Once initiated, the crack grows incrementally with each loading cycle. This stage is often characterized by the formation of striations on the fracture surface, each striation representing one cycle of advance. The rate of crack propagation (da/dN) is a key parameter in life prediction models.
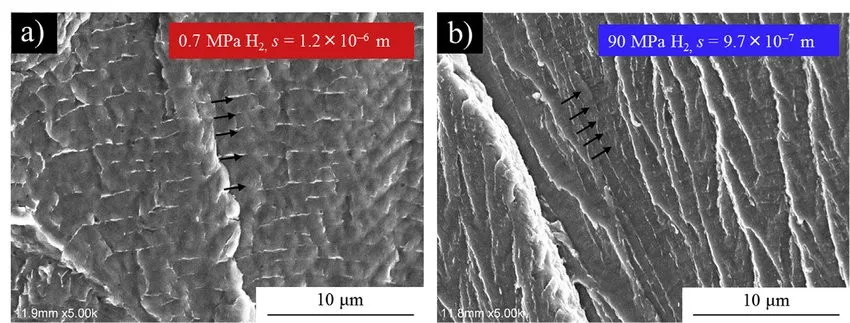div class="caption">Figure 2: SEM micrograph of a fatigue fracture surface showing distinct fatigue striations.
1.3 Final Fracture
When the propagating crack reduces the remaining cross-sectional area to a point where it can no longer support the applied load, sudden and catastrophic fast fracture occurs. This final stage is governed by the material's fracture toughness.
2. Factors Influencing Fatigue Behavior
The fatigue life of a metallic material is not an intrinsic property but is highly dependent on a multitude of factors:
| Factor Category | Specific Factors | Effect on Fatigue Life |
|---|---|---|
| Loading Conditions | Stress amplitude, mean stress, loading frequency, spectrum (constant vs. variable amplitude) | Higher stress amplitude and tensile mean stress significantly reduce fatigue life. |
| Material Properties | Ultimate tensile strength, microstructure (grain size, phases), surface condition, residual stresses | Finer grain sizes and compressive surface residual stresses generally improve fatigue life. |
| Environmental Conditions | Temperature, corrosive atmosphere (leading to corrosion fatigue) | Elevated temperatures and corrosive environments can drastically accelerate fatigue damage. |
| Geometric Factors | Notches, holes, surface roughness | Stress concentrators are prime sites for crack initiation, severely reducing fatigue life. |
3. Fatigue Life Prediction Methodologies
Accurately predicting the number of cycles to failure is essential for design and maintenance. Several approaches are commonly used, ranging from simple empirical methods to complex physics-based models.
3.1 Stress-Life (S-N) Approach
The S-N method is the oldest and most straightforward approach, primarily used for high-cycle fatigue (HCF) where stresses are primarily elastic. Tests are conducted on smooth specimens at different stress amplitudes (S) to determine the number of cycles to failure (N). The results are plotted on an S-N curve (Wöhler curve). A fatigue or endurance limit may exist for some metals (e.g., ferrous steels), below which failure theoretically does not occur.
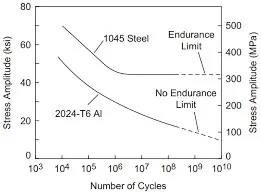div class="caption">Figure 3: A typical S-N curve for steel, illustrating the relationship between stress amplitude and cycles to failure, including the endurance limit.
3.2 Strain-Life (ε-N) Approach
For low-cycle fatigue (LCF) scenarios involving significant plastic deformation, the strain-life approach is more appropriate. It relates the total strain amplitude to fatigue life. The Coffin-Manson relationship is a cornerstone of this method, describing the plastic strain component's contribution to fatigue damage.
3.3 Fracture Mechanics Approach
This method focuses on the crack propagation stage. It uses Linear Elastic Fracture Mechanics (LEFM) principles, with Paris' Law being the most famous model: da/dN = C(ΔK)^m, where da/dN is the crack growth rate, ΔK is the stress intensity factor range, and C and m are material constants. This approach is crucial for damage-tolerant design, where the presence of initial flaws is assumed.
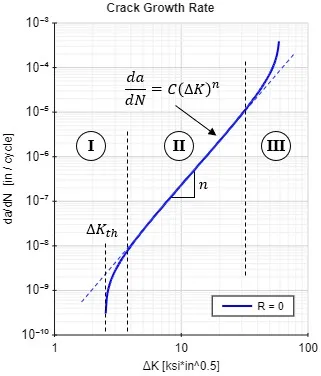div class="caption">Figure 4: Schematic of a Paris Law curve, depicting the three regions of crack growth behavior.
3.4 Energy-Based and Probabilistic Methods
Advanced methods include energy-based criteria, which consider the energy dissipated during cyclic loading, and probabilistic models that account for the inherent scatter in fatigue data to predict failure probabilities.
4. Conclusion
The study of fatigue behavior in structural metallic materials is a complex but vital field of materials science and engineering. While significant progress has been made in understanding the mechanisms and developing predictive models like S-N curves and fracture mechanics, challenges remain. These include accurately modeling variable amplitude loading, environmental interactions, and the behavior of advanced materials like high-entropy alloys. Continued research, combining experimental characterization with computational modeling, is essential for enhancing the safety and efficiency of future engineering systems.
