Theoretical Modeling of Superconducting Functional Materials
Introduction to Superconductivity and Functional Materials
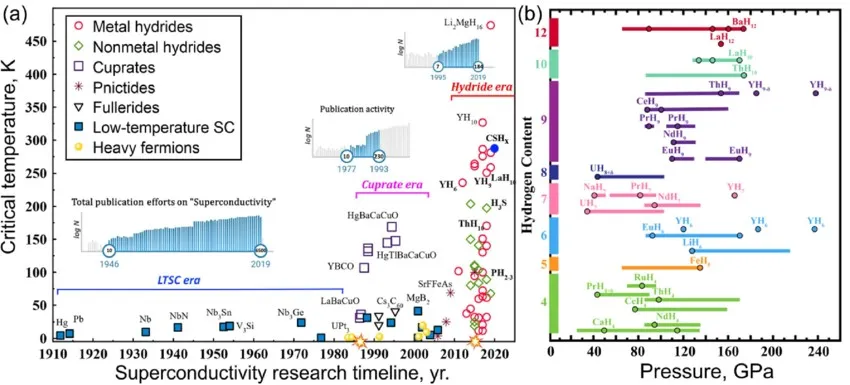
Superconducting functional materials represent one of the most fascinating areas in condensed matter physics, characterized by their ability to conduct electric current with zero resistance below a critical temperature. The theoretical modeling of these materials has evolved significantly since the discovery of superconductivity by Heike Kamerlingh Onnes in 1911. Modern computational approaches now enable researchers to predict new superconducting compounds, understand microscopic mechanisms, and design materials with enhanced properties for practical applications.
Fundamental Theoretical Frameworks
BCS Theory and Its Extensions
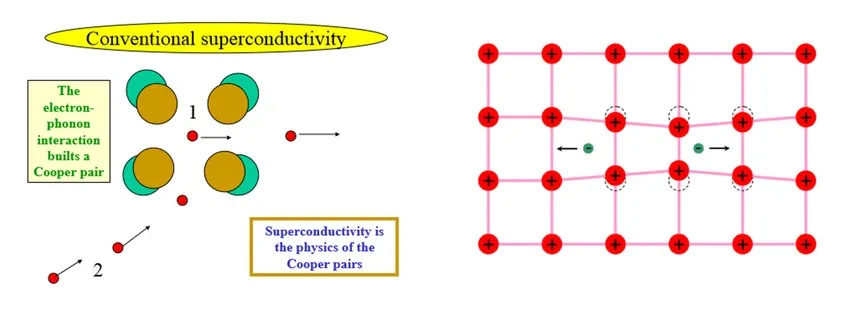
The Bardeen-Cooper-Schrieffer (BCS) theory, developed in 1957, provides the foundational understanding of conventional superconductivity. This theory explains how electrons form Cooper pairs through electron-phonon interactions, leading to the superconducting state. The BCS gap equation describes the temperature dependence of the superconducting energy gap:
Δ(T) = 1.76 kBTc tanh(1.74 √(Tc/T - 1))
where Δ is the energy gap, kB is Boltzmann's constant, and Tc is the critical temperature. Modern extensions of BCS theory incorporate strong-coupling effects, multiband superconductivity, and non-phononic pairing mechanisms.
Ginzburg-Landau Theory
The Ginzburg-Landau theory provides a phenomenological approach to superconductivity, particularly useful for understanding the behavior of superconductors in magnetic fields and near phase transitions. The theory introduces a complex order parameter ψ that describes the superconducting state, with the free energy density expressed as:
fs = fn + α|ψ|2 + (β/2)|ψ|4 + (1/2m*)|(-iħ∇ - 2eA/c)ψ|2 + B2/8π
This framework successfully predicts phenomena such as flux quantization and the Meissner effect.
Advanced Computational Methods
Density Functional Theory for Superconductors
Density Functional Theory (DFT) has been extended to describe superconducting materials through the development of superconducting DFT (SCDFT). This approach allows for first-principles calculations of superconducting properties, including critical temperatures and gap structures. The methodology combines Kohn-Sham equations with the superconducting gap equation, enabling parameter-free predictions of superconducting properties.
| Method | Accuracy | Computational Cost | Applications | Limitations |
|---|---|---|---|---|
| DFT+U | Medium | Low-Medium | Strongly correlated systems | U parameter dependence |
| SCDFT | High | High | Conventional superconductors | Limited to phonon-mediated pairing |
| DMFT | Very High | Very High | Heavy fermion systems | Extremely computationally expensive |
| Eliashberg Theory | High | Medium-High | Strong-coupling superconductors | Requires input from other methods |
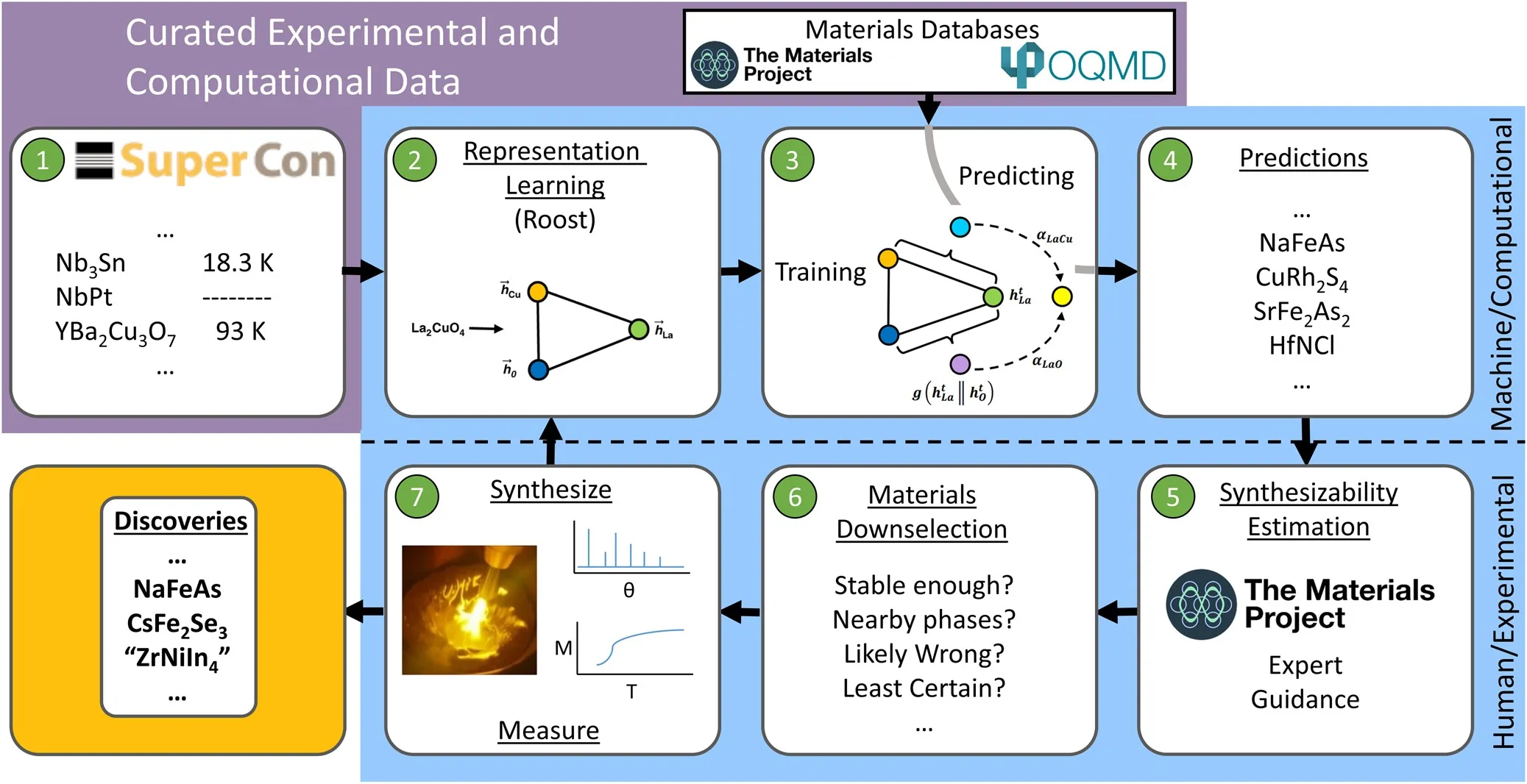
Machine Learning Approaches
Recent advances in machine learning have revolutionized the theoretical modeling of superconducting materials. Neural networks and other ML algorithms can predict superconducting critical temperatures, identify promising material candidates from large databases, and optimize material compositions. These approaches significantly accelerate the discovery process and provide insights that complement traditional theoretical methods.
Modeling Unconventional Superconductors
High-Temperature Cuprate Superconductors
The theoretical modeling of high-temperature cuprate superconductors remains one of the most challenging problems in condensed matter physics. Various approaches have been developed, including the t-J model, Hubbard model, and resonating valence bond (RVB) theory. These models attempt to explain the d-wave symmetry of the superconducting gap and the unusual phase diagram featuring pseudogap and strange metal phases.
Iron-Based Superconductors
Iron-based superconductors represent another important class of unconventional superconductors. Theoretical modeling of these materials typically involves multiband approaches, as multiple Fermi surface sheets contribute to the superconducting state. The s± pairing symmetry, where the gap changes sign between electron and hole pockets, is widely supported by theoretical calculations and experimental evidence.
| Material Class | Maximum Tc (K) | Pairing Symmetry | Primary Pairing Mechanism | Theoretical Challenges |
|---|---|---|---|---|
| Elemental (Hg) | 4.15 | s-wave | Electron-phonon | None |
| Cuprates | 133 | d-wave | Electronic | Strong correlations, pseudogap |
| Iron-based | 55 | s±-wave | Spin fluctuations | Multiband physics |
| MgB2 | 39 | s-wave | Electron-phonon | Two-gap superconductivity |
| Hydrides | 250+ | s-wave | Electron-phonon | High-pressure phases |
Emerging Materials and Future Directions
Topological Superconductors
Topological superconductors represent an exciting frontier where superconductivity meets topological quantum computation. Theoretical modeling of these materials requires combining superconducting theory with topological band theory. Majorana zero modes, predicted to exist at the boundaries of topological superconductors, hold promise for fault-tolerant quantum computing.
Hydrogen-Rich Compounds
Theoretical predictions and subsequent discoveries of high-temperature superconductivity in hydrogen-rich compounds under high pressure have opened new avenues for research. Computational methods, particularly structure prediction algorithms coupled with electron-phonon calculations, have been instrumental in guiding experimental searches for these materials.
Two-Dimensional Superconductors
The discovery of superconductivity in two-dimensional materials, such as twisted bilayer graphene and transition metal dichalcogenides, has created new opportunities for theoretical modeling. These systems often exhibit unconventional superconducting phases that can be tuned by external parameters such as doping, pressure, and twist angle.
Challenges and Limitations in Theoretical Modeling
Despite significant progress, theoretical modeling of superconducting materials faces several challenges. Strong electron correlations in many unconventional superconductors make accurate calculations difficult. The competition between different ordered states (superconductivity, magnetism, charge order) requires sophisticated treatment. Additionally, the predictive power of current methods for new high-temperature superconductors remains limited, highlighting the need for continued theoretical development.
Conclusion
Theoretical modeling of superconducting functional materials has progressed remarkably, from phenomenological descriptions to first-principles computational approaches. The integration of traditional theoretical methods with machine learning and high-throughput computational screening promises to accelerate the discovery of new superconducting materials with enhanced properties. As theoretical frameworks continue to evolve, they will play an increasingly important role in guiding experimental research and developing practical applications of superconductivity in energy, transportation, and quantum information technologies.

